Fracture modeling of rocks with bedding planes

A dual-mechanism tensile failure criterion for transversely isotropic rocks

Tensile failure is a common failue mode in shale in engineering applications such as shale gas exploitation. Tensile for transversely isotropic rocks like shale is usually dependent on the bedding plane orientation in the material, and the Nova-Zaninetti criterion is commonly accepted as the tensile failure criterion with the best performance, which extends the Rankine criterion by constructing a bedding-orientation-dependent rock strength with a rank-two tensor to characterize the anisotropy in rock strength. Such a criterion can be fully calibrated with rock tensile strength along the bed-normal and bed-parallel directions, and the shape of the variation curve of rock tensile strength with bedding plane orientation is determined by the anisotropy ratio, defined as the ratio between rock strength along the bed-parallel direction and the bed-normal direction.

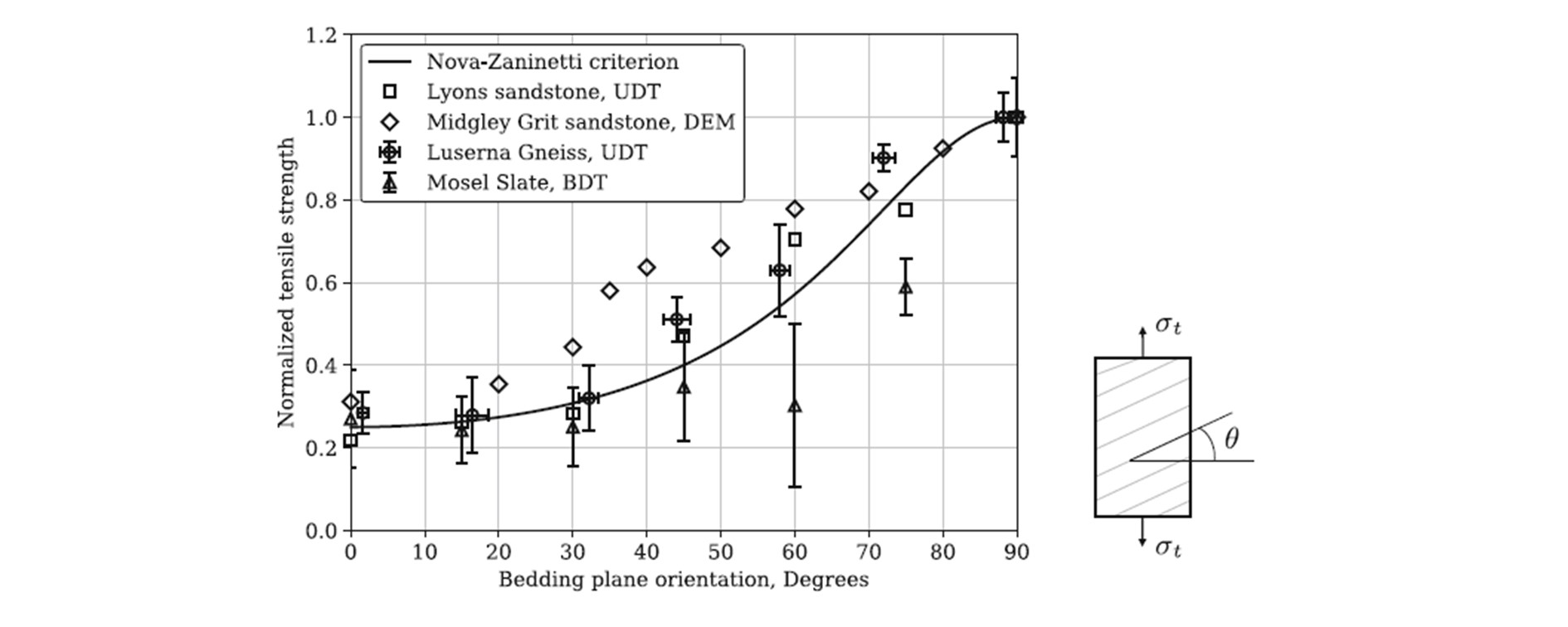
Variation of tensile strength with bedding plane orientation with an anisotropy ratio near 4.

The figure above illustrates the variation of tensile strength with bedding plane orientation for several kinds of transversely isotropic rocks with an anisotropy ratio near 4, and the prediction generated with the Nova-Zaninetti criterion. From the figure we can conclude that the Nova-Zaninetti criterion has the following shortcomes:

• The shape of variation curve of rock tensile strength predicted with the Nova-Zaninetti criterion is determined with a given anisotropy ratio, but in reality there can be different forms of the variation curves;
• For rocks with weakly-cemented bedding planes such as the Midgley Grit Sandstone, there exists a transition in the strength variation curve distinguishing failure along bedding planes or through rock matrix, which can not be reproduced by the Nova-Zaninetti criterion;
• It has been revealed in literatures that the prediction of failure plane orientation with the Nova-Zaninetti can hardly be regarded as perfect.

Faced with the limitations of the existing tensile failure criteria for transversely isotropic rocks, we developed a novel two-mechanism tensile failure criterion that can overcome these issues[1]. For failure through anisotropic rock matrix, we also extended the Rankine criterion to reflect the impact of material anisotropy. Rather than finding a direct expression of the bedding-orientation-dependent rock strength, we instead extend the stress measure with an alternative stress transformed with a rank-four projection tensor. Failure criterion for anisotropic rock matrix developed in this manner has a more general application range than the Nova-Zaninetti criterion, as for a given anisotropy ratio, there can be various forms of the strength variation curve with bedding plane orientation.

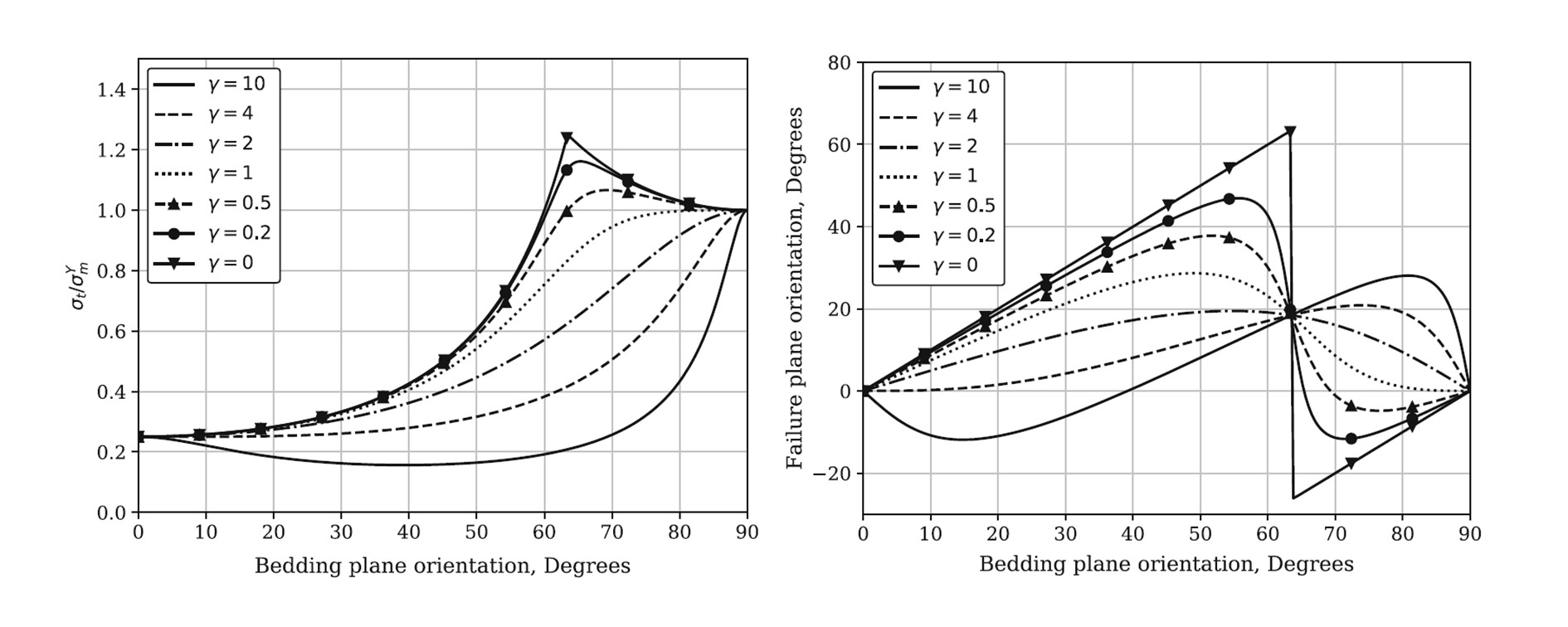
Variation of (left) tensile strength (right) failure plane orientation with bedding plane orientation with an anisotropy ratio equal to 4, given different shape parameter ɣ.

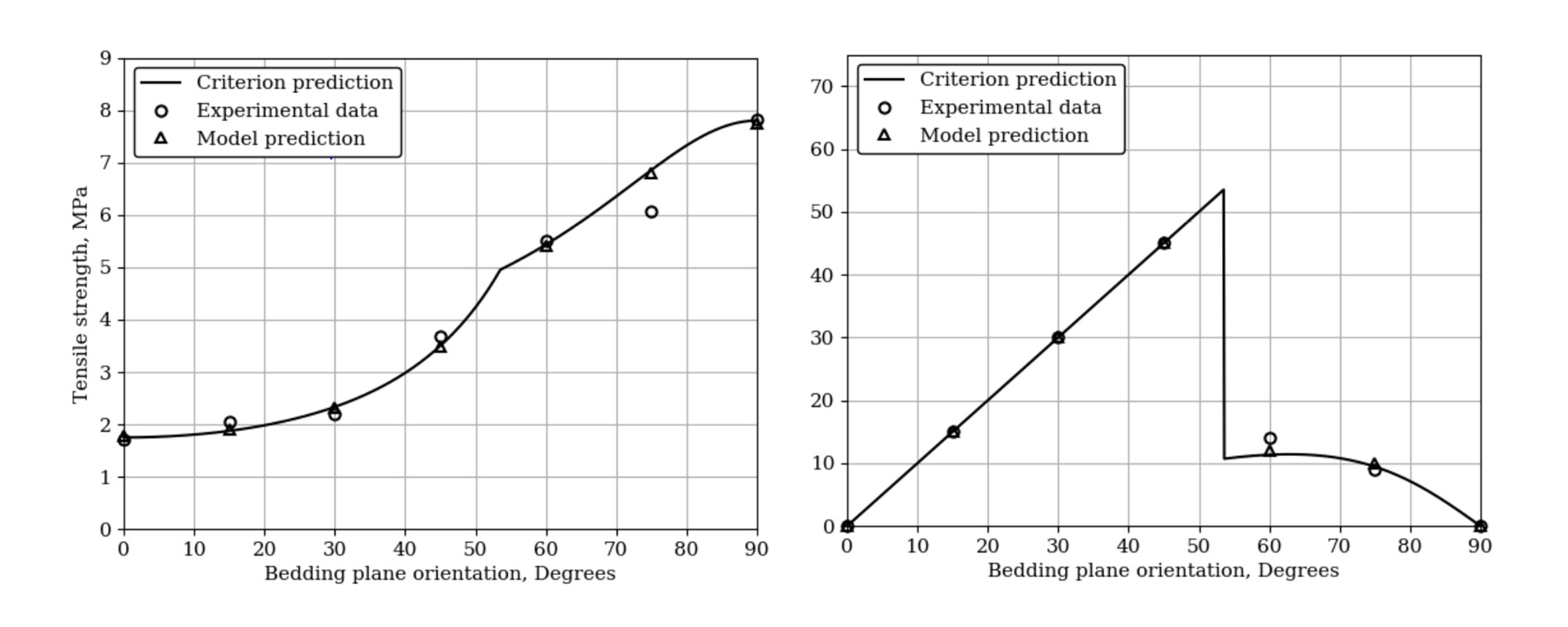
For failure along the bedding planes, we treat it seperately and constructed the tensile criterion based on the normal component of stress on the bedding planes. We applied the proposed failure criterion and calibrated the model with the response of Lyons Sandstone. As one can conclude from the following figures, the proposed criterion can generate a better fit to experimental data for both the variation of tensile strength and failure plane orientation with bedding plane orientation.

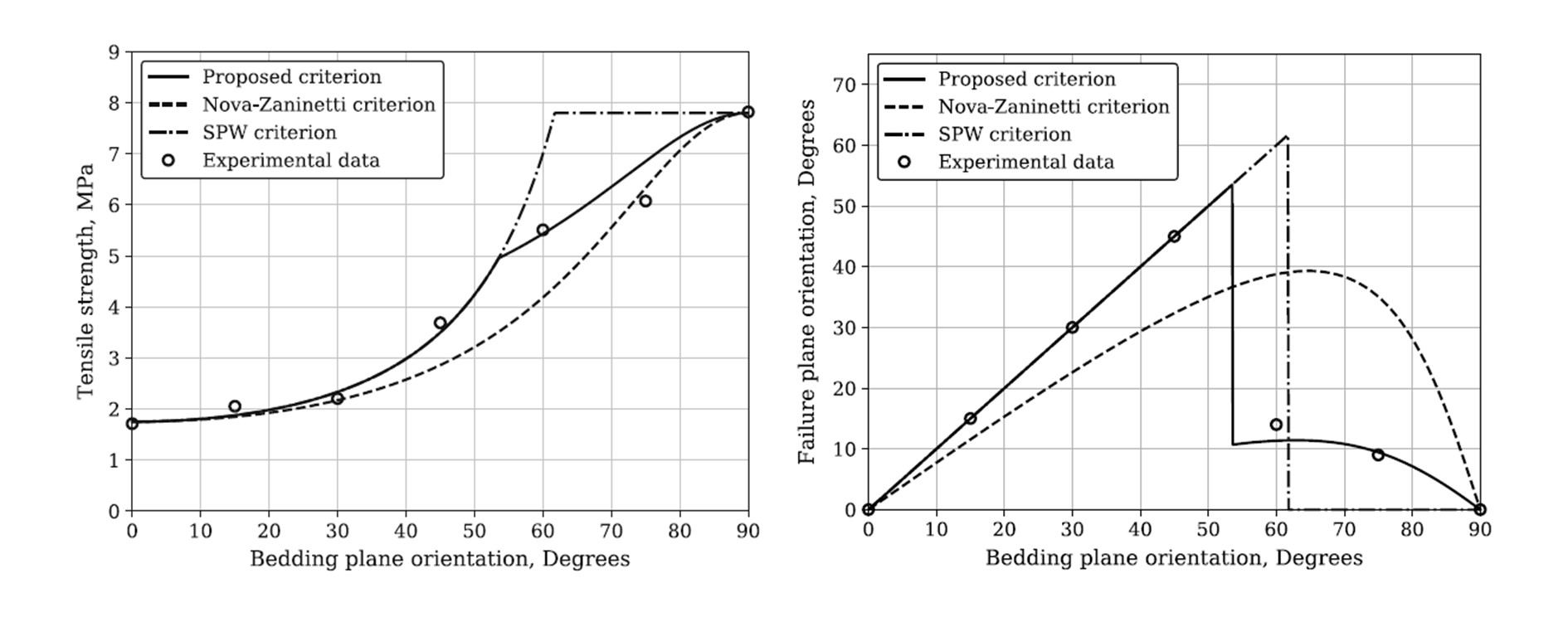
Variation of (left) tensile strength (right) failure plane orientation with bedding plane orientation for Lyons Sandstone.

Phase-field modeling of tensile fracturing processes in transversely isotropic rocks

One of my ongoing work is to cast the dual mechanism failure criterion into the phase-field fracture modeling framework and develop a computational tool for boundary-value problem simulations that involve tensile failure of transversely isotropic rocks[2]. By assigning each failure mechanism a distinct phase-field variable, we can describe failure through rock matrix or along weak bedding planes separately.

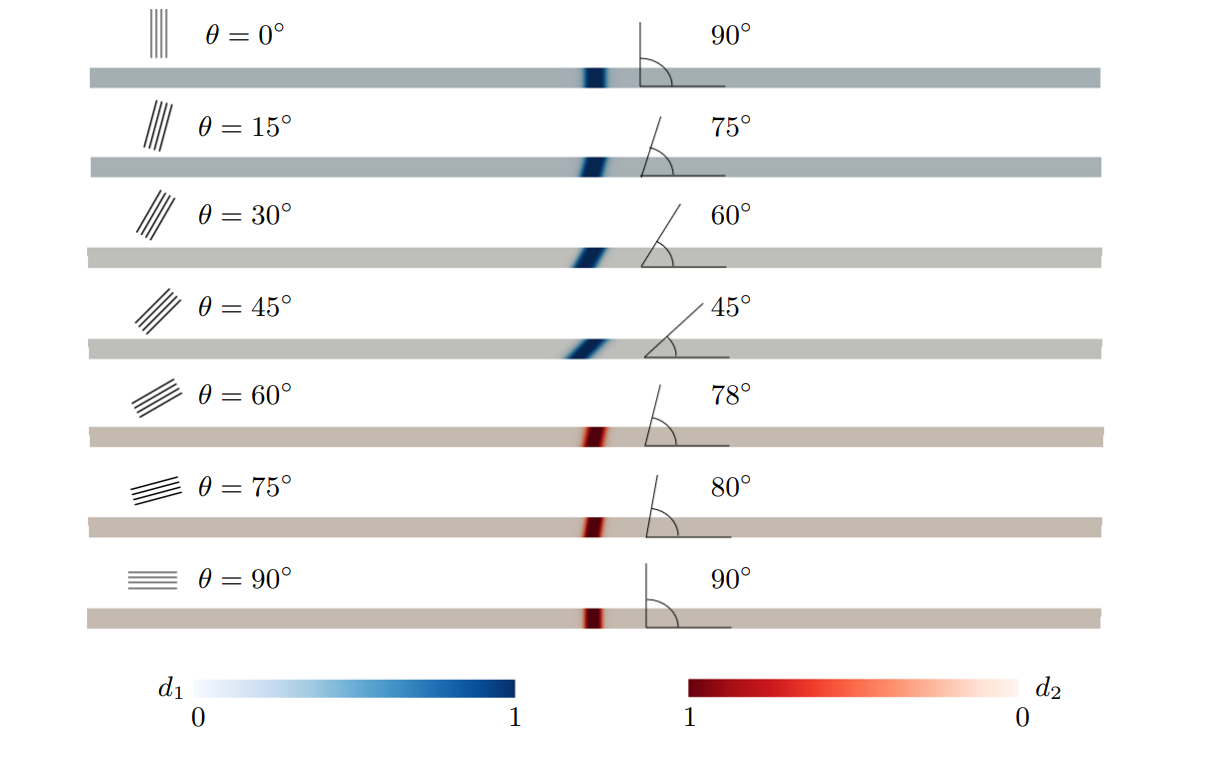
The ensuing figures demonstrate a benchmark test to validate the implementation of the phase-field model, where we tried to reproduce the response of Lyons Sandstone in uniaxial tension test. As one can see in the following figure, tensile crack tends to propagate along the bedding planes (represented by d₁) when the bedding plane orientation is mild, and to propagate through the rock matrix (represented by d₂) when the bedding plane orientation is steep in the specimen.

fracture patterns generated with phase-field fracture simulation schemes.

We also made a comparison of the rock tension strengh and failure plane orientation predicted with the phase-field model and the failure criterion. As one can see in the following figure, the results are perfectly aligned, indicating that our implementation is valid.

Variation of (left) tensile strength (right) failure plane orientation with bedding plane orientation for Lyons Sandstone.

Reference:

[1] Zhao Y., Wang R., Zhang J.M.* (2022). A dual-mechanism tensile failure criterion for transversely isotropic rocks. Acta Geotechnica, 17(11), 5187-5200.
[2] Yuan W.H., Zhao Y.*, Zhang B.Y., A stress-based double-phase-field framework for tensile fracturing process in transversely isotropic rocks, manuscript in preparation.