Poromechanical modeling of coupled solid deformation-fluid flow in shale
Coupled solid deformation-fluid flow in anisotropic elastoplastic media
The effective stress concept and the poromechanical framework pioneered by Terzaghi and Biot have been widely adopted to illustrate coupled fluid flow and solid deformation in porous rocks, but there were still some links missing for anisotropic and ductile rocks like shale. There hardly exists complete discussions in existing research work on poromechanical formulations that consider material anisotropy, elastoplastic, and grain compressibility, and they are all critical components in quantifying the hydromechanical processes in transversely isotropic rocks. Based on the mixture theory and continuum thermodynamics, I derived a novel mathematical framework for coupled solid deformation and fluid flow with all of the aforementioned factors addressed[1].
The proposed framework involves a new set of governing equations for mass conservation of fluid and solid, and a new effective stress formulation that identifies distinct forms of effective stress for elastic response and plastic response respectively. Coefficients that emerge in the governing equations are evaluated naturally through the derivation, thus the proposed framework won’t require any additional constitutive law or assumption for parameter evaluation. For this work, I also developed a mixed finite element framework for its numerical implementation and conducted simulations of a consolidation problem with strip loading to reveal the unique hydromechanical response in anisotropic elastoplastic porous rocks, as demonstrated in the ensuing figures.
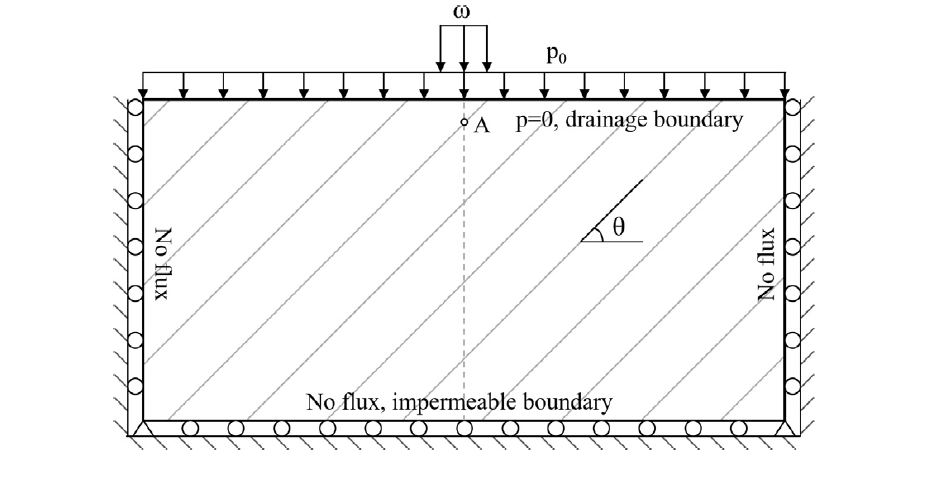
Setup of the consolidation problem in a transversely isotropic medium under a strip load.
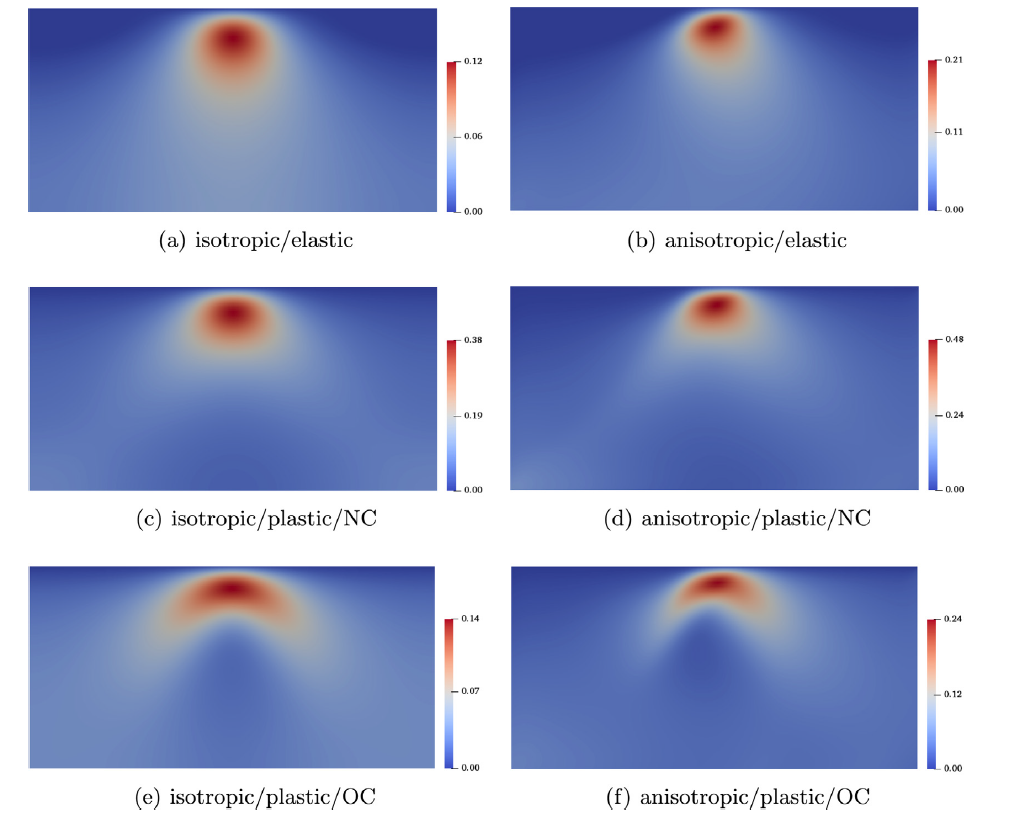
The figures below demonstrate the influence of elastoplasticity on the consolidation process in the domain. In elastic domain, the pore pressure build-up and the ground settlement is the least, while for normally consolidated medium with pc0=-1MPa, the material is the weakest and the domain undergoes largest pore pressure accumulation and ground settlement. For overconsolidated medium with pc0=-2MPa, the evolution of pore pressure and ground settlement lie in between the other two scenarios.
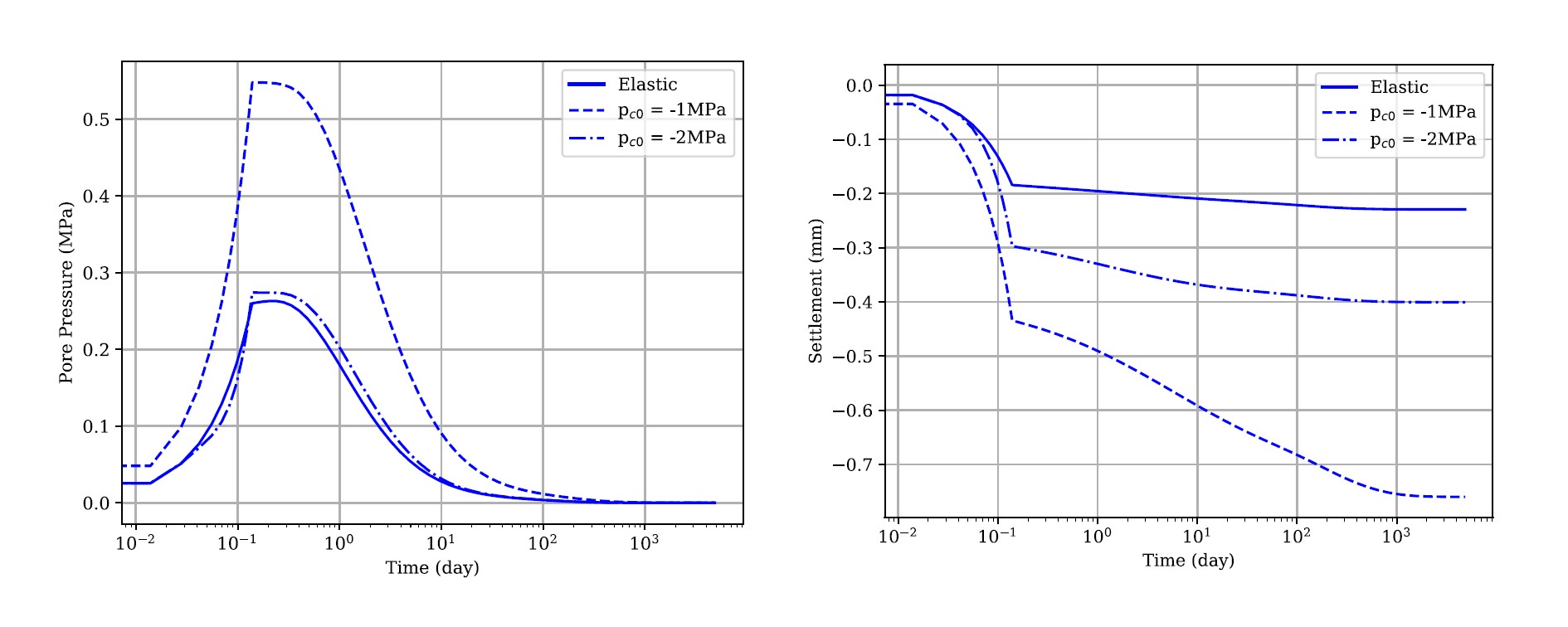
Evolution of ground settlement and pore pressure.
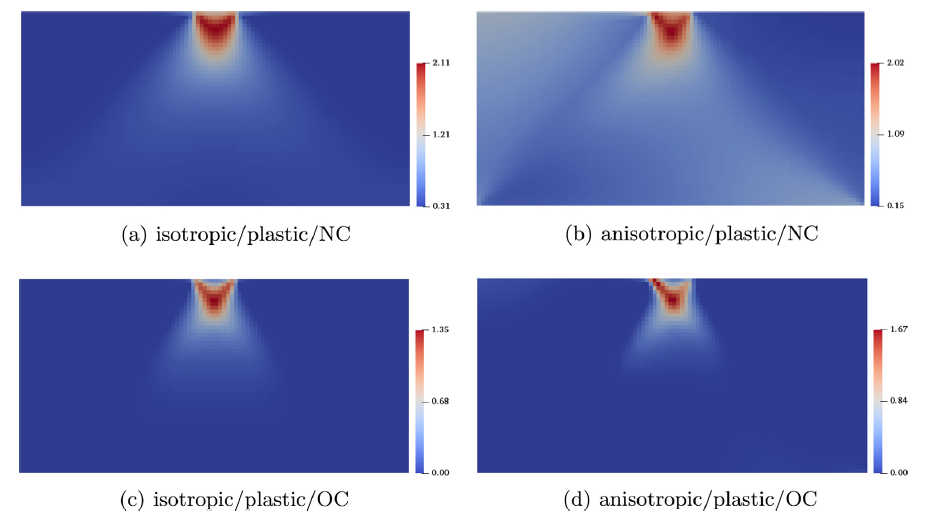
The following two sets of figures demonstrate contours of pore pressure and Darcy velocities for various cases, where a unique response in domains made up of overconsolidated materials has been observed. For such cases, plastic dilation in regions beneath the strip load leads to an arc-shaped pore pressure distribution accompanied with and an eddy-shaped Darcy velocity distribution.
Contour of pore pressure in the medium for various scenarios.
Vectors of Darcy velocities in the medium for various scenarios.
The figures below shows contours of plastic deformation in both normally consolidated and overconsolidated domains. For normally consolidated domains, plastic deformation would occur in the region beneath the strip load, as within these area the material is consolidating and getting stronger. For overconsolidated domains, however, two crossing shear bands will form beneath the strip load.
Contour of norm of plastic strain in the medium for various scenarios.
Poromechanical modeling of anisotropic elastoplastic media with double porosity
I have developed a novel continuum poromechanical framework for shale considering the bimodal pore size distribution from the existing form of voids in shale as either microcracks or nanopores. Specifically speaking, I extended the framework discussed in the previous section with the double porosity theory, which allows for the consideration of different permeability and constitutive law for fluid flow at different pore scales[2]. This work is the first of its kind to integrate factors including anisotropy, elastoplasticity, and double porosity in the analysis of hydromechanical responses of shale.
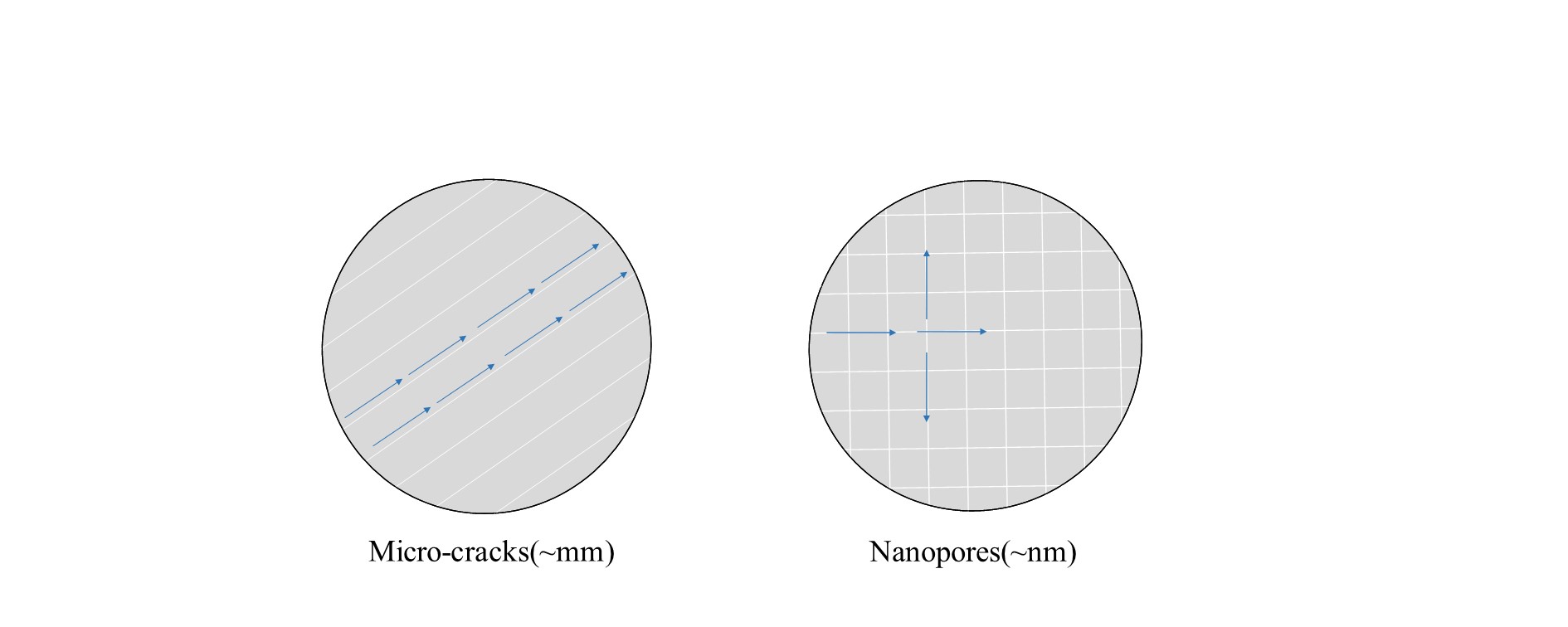
Illustration of the double porosity concept.
The figure above demonstrates the concept of double porosity, where the voids can be separated into two continuous porous network consists of pores with different length scales. In macropores made up of microcracks, we consider the fluid flow inside is anisotropic, with a preferred flow direction along the crack planes. In micropores, we assume the fluid flow is isotropic. With this proposed framework, I reproduced the 1-D consolidation process of Opalinus shale, and the setup of the problem as well as the loading protocol is demonstrated in the figure below:
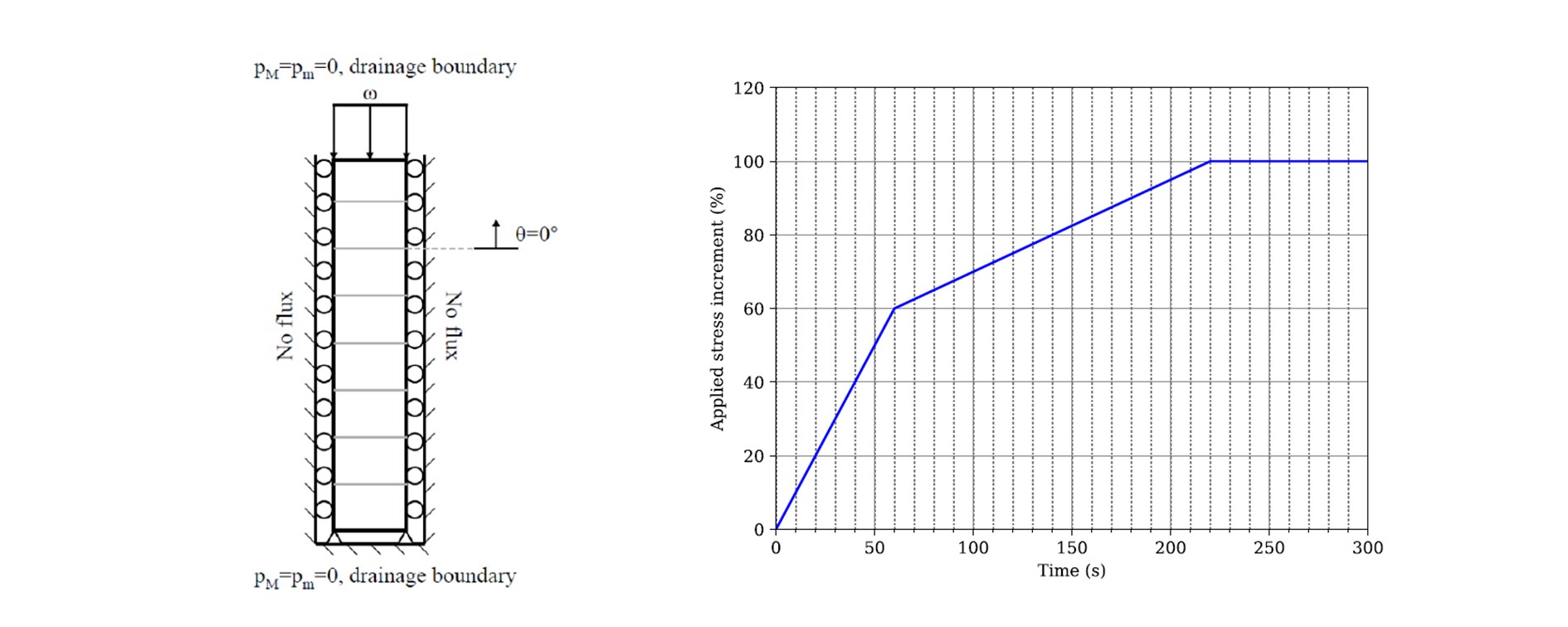
Setup of the 1d consolidation problem in Opalinus Shale.
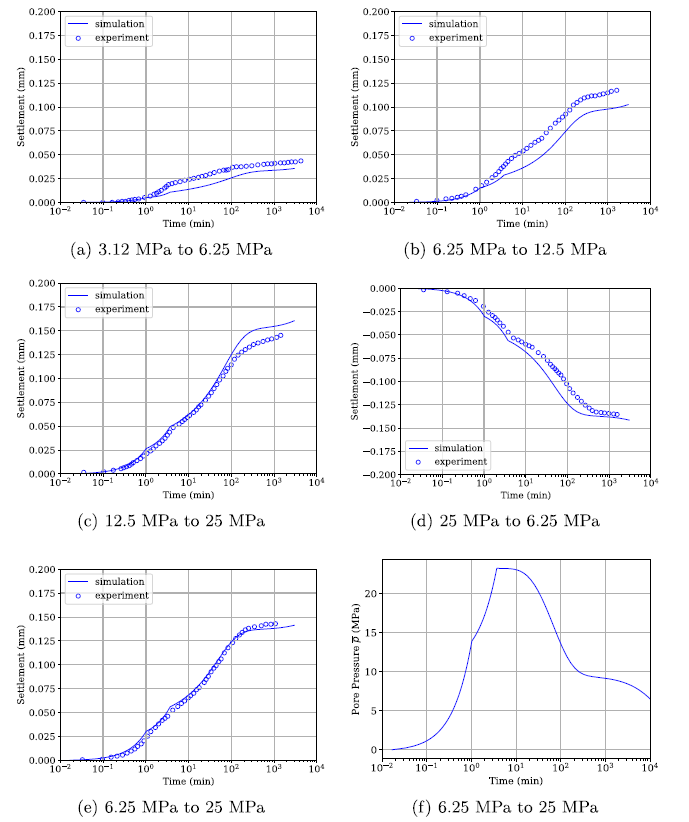
As one can tell from the results, for each loading stress, both the primary and the secondary consolidation processes can be captured with the proposed framework, which correspond to the dissipation of pore pressure in macropores and in micropores respectively.
Evolution of ground settlement given different overburns.
Reference:
[1] Zhao Y., Borja R.I.* (2020). A continuum framework for coupled solid deformation–fluid flow through anisotropic elastoplastic porous media. Computer Methods in Applied Mechanics and Engineering, 369, 113225.
[2] Zhao Y., Borja R.I.* (2021). Anisotropic elastoplastic response of double-porosity media. Computer Methods in Applied Mechanics and Engineering, 380, 113797.